Basic Inputs

Definition of basic parameters of the rotating group and pump operating conditions:

Parameter	Symbol	Units	Notes
Number of pistons	z	-	Takes integer values between 1 and 99 and needs to satisfy z_max equation.
Piston diameter	dp	mm	Must be positive value
Piston pitch diameter	Dp	mm	Has to be greater than piston diameter d_p
Swashplate angle	β	degree	Typical value below 23 degrees for axial piston machines.

Must be positive

Parameter	Symbol	Units	Notes
Outlet pressure	HP	bar	Must be positive
Inlet pressure	LP	bar	Must be positive
Speed	n	rpm	-

Angle between each piston is (2π/z)

The simulation is only run for numerically possible designs when the wall thickness wt between bores is greater than 0. For a given piston diameter d_p and piston pitch diameter D_p, the maximum number of pistons z is defined by assuming a wall thickness of zero and round down to closeset integer:

z_max = ⌊ π / arcsin((d_p) / D_p) ⌋

Actual wall thickness according to input data is caluclated based on the following:

wt = D_p * sin (π / z) - d_p [mm]

General

Simulation of the main pump characteristics:

Geometric displacement of the pump

The geometric displacement volume V_g of an axial piston pump is a function of basic dimensions:

V_g = (π · dp² / 4) · Dp · tanβ · z / 1000 [cc/rev]

Theoretical outlet pump flow

The theoretical pump flow is the product of displacement volume and speed:

Q_theo = (V_g · n) / 1000 [l/min]

Theoretical input shaft torque

The theoretical input torque is a product of geometric displacement volume V_g and differential pressure between inlet and outlet lines (Δp = HP − LP):

T_theo = (Δp · V_g) / (20π) [N.m]

Theoretical input power

P_in = (T_theo · n · π) / 30000 = (Q_theo · Δp) / 600 [kW]

Kinematic flow

Simulation of the continuous flow:

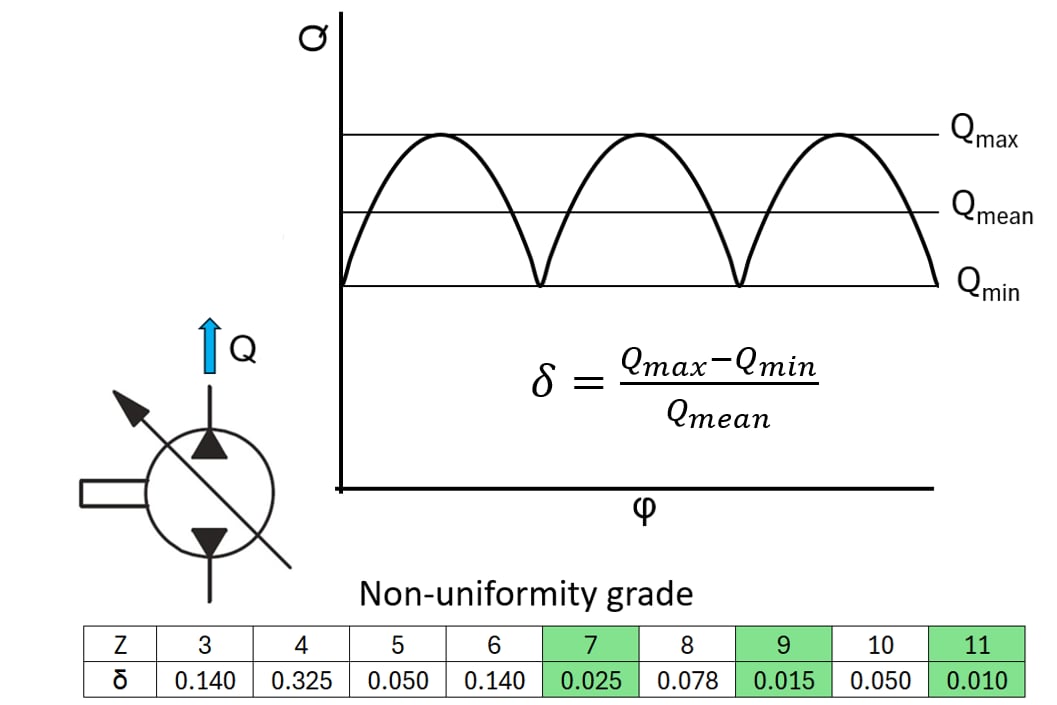
The graph in "Kinematic Flow" tab shows the flow rate of each piston and the total output flow Q of the pump during one shaft revolution. The pump flow rate is not constant but pulsating and is a function of each piston area and speed v_pi. The mean value corresponds to the theoretical flow rate of the pump Q_theo.

Q = ∑_i=1^z (π · d_p² / 4) · v_pi · 6e-2 [l/min]

Non-uniformity grade δ characterizes the flow pulsation.

Torque

The graph in "Torque" tab shows the torque from each piston and the total input torque of the pump during one shaft revolution. The pump flow rate is not constant but pulsating. The mean value corresponds to theoretical input shaft torque T_theo.

T = D_b / 2 · tanβ · ∑_i=1^z (π · d_p² / 4) · p_DCi(φ_i) · sinφ_i · 1e-4 [N.m]

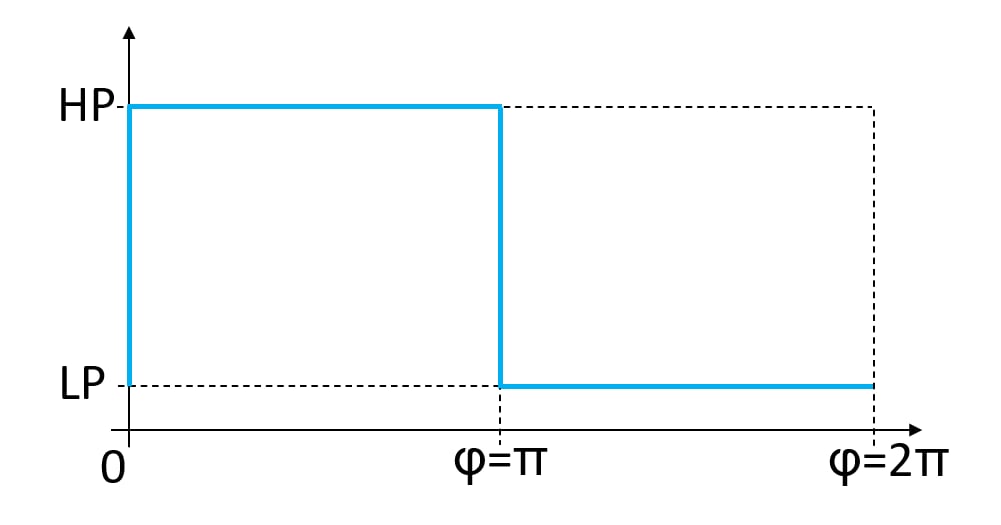
Simulation considers ideal displacement chamber pressure behavior:

Axial Piston pump flow rate and torque calculations - ideal displacement chamber pressure

Piston kinematics

Simulation of piston kinematic parameters during one shaft revolution

Piston stroke

The piston displacement sp is proportional to the pitch diameters of pistons Db, the swash plate angle β and on actual angular position φ:

s_p(φ, β) = − (Dp / 2) · tanβ · (1 − cosφ) [mm]

Piston speed

Axial velocity of individual piston-slipper subassembly v_p is derived from the piston stroke and its angular position φ:

v_p(φ, β) = (ds_p/dφ) · ω = −ω · (Dp / 2) · tanβ · sinφ / 1000 [m/s]

Where ω is shaft angular velocity.

Piston acceleration

Further derivation yields an acceleration of the piston-slipper subassembly a_p:

a_p(φ, β) = (dv_p/dφ) · ω = −ω² · (Dp / 2) · tanβ · cosφ / 1000 [mm/s²]

Output Data

The simulation results summary in tabular format. You can copy the data by clicking the icon